Improving Deadline Protocols - Censorship.wtf

Deadline protocols (1:20)

Ethereum has some resistance to censorship but still has non-ideal worst case censorship times.

Censorship detection can improve deadline protocols even if censorship prevention is not perfect. Being able to detect censorship on-chain allows protocols to be more efficient.

Deadline protocols require parties to act before a deadline, otherwise they are disadvantaged. Examples are on-chain auctions, interactive protocols with defaults if no action, fraud proofs and optimistic rollups, and veto mechanisms in side chains.

If honest parties can't meet a deadline due to censorship, deadline protocols don't work as well.

Censorship detection allows deadline protocols to account for potential censorship rather than assuming parties can always meet deadlines.

Threat model (2:45)

The threat model involves an adversary targeting a specific deadline protocol to censor certain transactions.

The adversary aims to compromise Ethereum block proposers/builders by becoming them, paying them off, or attacking them.

The goal is to control a fraction of proposing/building activity, and the motive is financial gain by corrupting the deadline protocol operation.

Examples: In an auction, bid low and censor higher bids. In an optimistic rollup, make a false claim and censor disagreements.

Main assumptions :

• Adversary targets a specific deadline protocol
• Tries to compromise/control Ethereum block proposers/builders
• Seeks financial gain by censoring transactions to corrupt the deadline protocol

Common responses (4:30)

In low stakes protocols, we can ignore the censorship issue or make deadlines longer. This may be rational if an attack is unlikely or the tradeoff favors responsiveness.

In high stakes protocols, longer deadlines or ignoring the issue is insufficient.

The usual approach is to make the deadline longer than the worst case assumed censorship time.

On Arbitrum, the dispute deadline is 7 days, because that's the assumed worst case censorship attack on Ethereum that wouldn't trigger a social response. 7 days is too long, but necessary in Arbitrum where billions could be stolen via a censorship attack.

The goal is to improve high stakes protocols by detecting censorship, rather than just assuming worst case censorship and having very long deadlines.

Key idea (6:40)

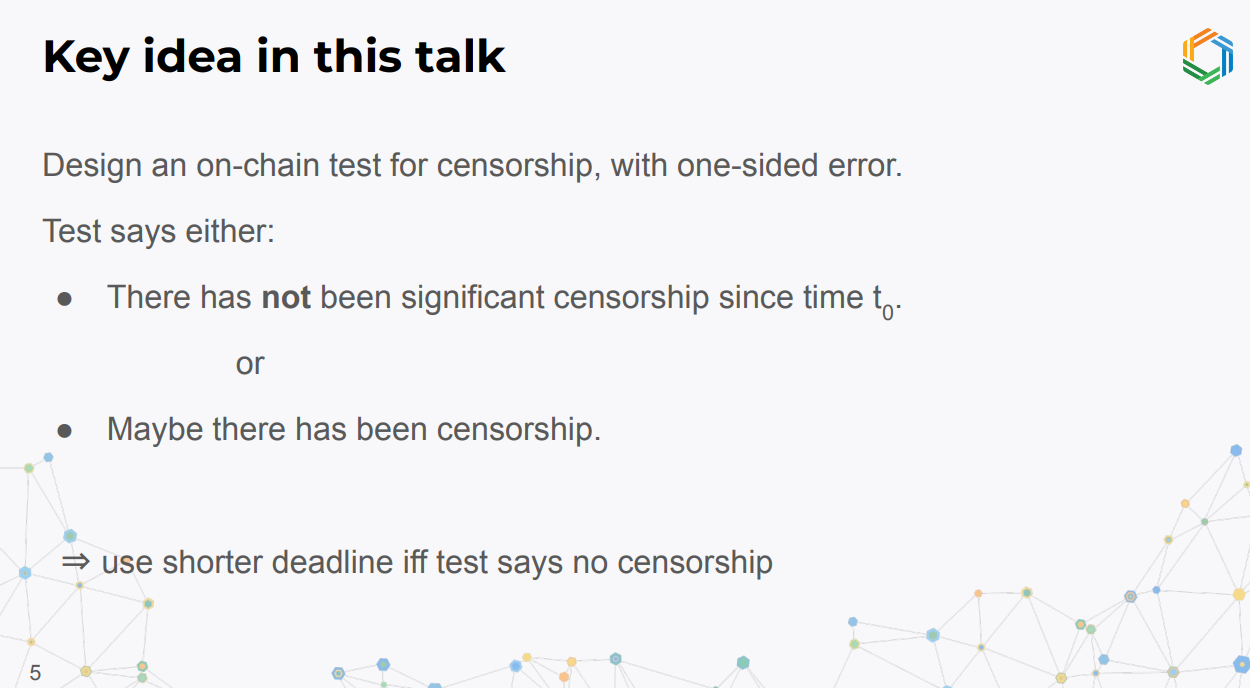
The main idea is to design an on-chain test for Ethereum censorship with one-sided error.

The test will say either no significant censorship or maybe censorship. It is designed to be statistically confident when saying no censorship.

In a deadline protocol, the deadline can be shortened if the test says no censorship. For example, a normal 7 day deadline could become 3 hours if the test shows no censorship for 3 hours.

It's not possible to definitively detect censorship, but it is possible to detect a lack of censorship. This allows protocols to dynamically shorten deadlines when censorship is not detected.

Censorship attacks on Ethereum (8:30)

There are two levels of censorship attacks on Ethereum :

1. Weak censorship - Block proposers refuse to include target transactions
2. Strong censorship - Blocks with target transactions are rejected or reorged

Weak censorship can be defeated as long as some proposers are honest. Strong censorship can sustain attacks if the attacker controls enough proposer/builder power

Defeating weak censorship (9:55)

Let's assume :

• A fraction f of proposers are honest and will include a target transaction
• x = number of honest slots out of n total slots
• Probability that x ≤ k follows a binomial distribution based on f

This models it as a weighted coin flip with probability f of being honest. So with enough honest proposers, weak censorship can be statistically defeated, but strong censorship is harder to overcome if the attacker has lots of control

Strong censorship (11:25)

Strong censorship involves suppressing honestly produced blocks, assuming the adversary controls enough proposer power.

For a successful attack, the adversary must turn every honest slot into an empty slot in the canonical chain. Therefore, if an attack succeeded, the number of honest slots ≤ number of empty slots.

We can measure empty slots on-chain by looking at timestamp advances and number of blocks added :

• Let x = honest slots
• y = empty slots out of n total slots.
• If an attack occurred, P(y < k) ≤ P(x ≤ k) based on the honest proposer fraction f.

This allows an on-chain statistical test of whether a successful strong attack occurred by comparing empty slots to the binomial distribution.

If the number of empty slots is statistically much lower than expected with no attack, we can conclude no strong attack occurred recently.

In practice (14:30)

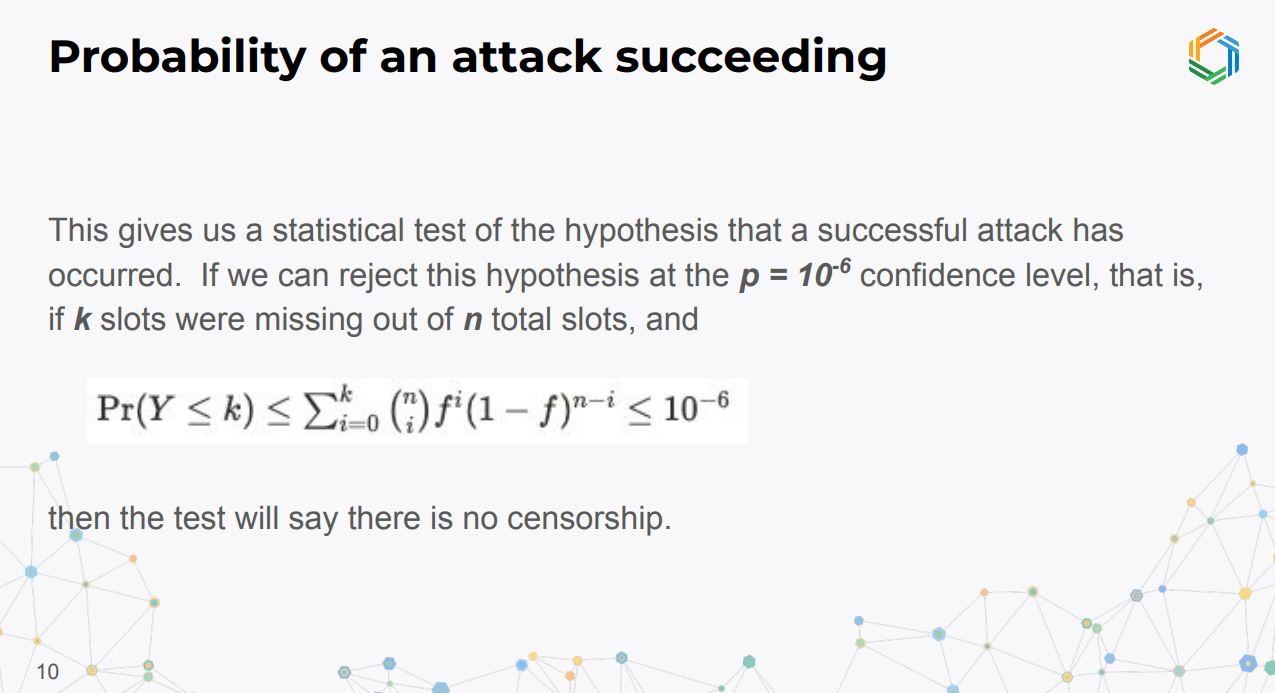
If we can reject the attack hypothesis with extremely high confidence (e.g. p < 10^-6), the test can conclude no censorship.

Given k empty slots out of n total slots, and assumed honest proposer fraction f, we can check if the inequality holds.

To implement it:

• Choose parameters f, k, n in advance
• Precompute the binomial summation offline
• Build a simple on-chain test to check if k and n satisfy the inequality

Example with 10% honest proposers : No censorship if ≤ 34 empty slots out of 688 total slots (2h 18m), or if ≤ 4 empty slots out of 225 total slots (45 min)

These tests would have always passed in Ethereum's history since the Merge.

Some annoying issues (16:15)

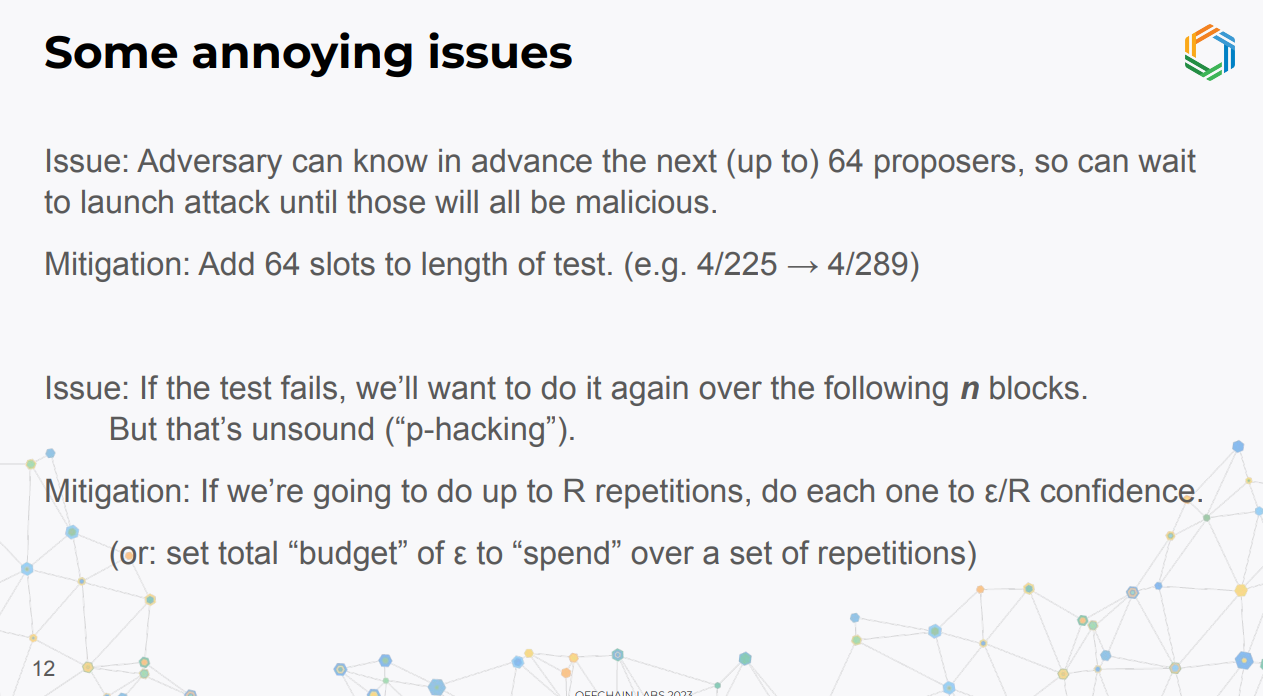
Issue 1 : Adversary may know next few proposers so can wait to attack when they are friendly.

Mitigation : Add 64 empty slots to the beginning of the test period, assuming the adversary can't arrange for no empty slots in the first 64.

Issue 2: Repeatedly testing until it succeeds is statistically unsound (p-hacking).

Mitigation : Set confidence level for each test to epsilon/r if doing up to r repetitions, or set a total epsilon budget and spend it over repetitions.

We have to make sure not to keep testing until it succeeds, as that compromises statistical validity.