Distributed Blockbuilding Networks

Blockchain networks like Bitcoin and Ethereum are made up of blocks that contain transaction information. Traditionally, only a few powerful computers build these blocks, which goes against blockchain's goal of decentralization.

Hernan (the speaker) wants to explore using an optimization method called the "knapsack problem" to allow more computers to participate in block building.

Block building as a knapsack problem (0:50)

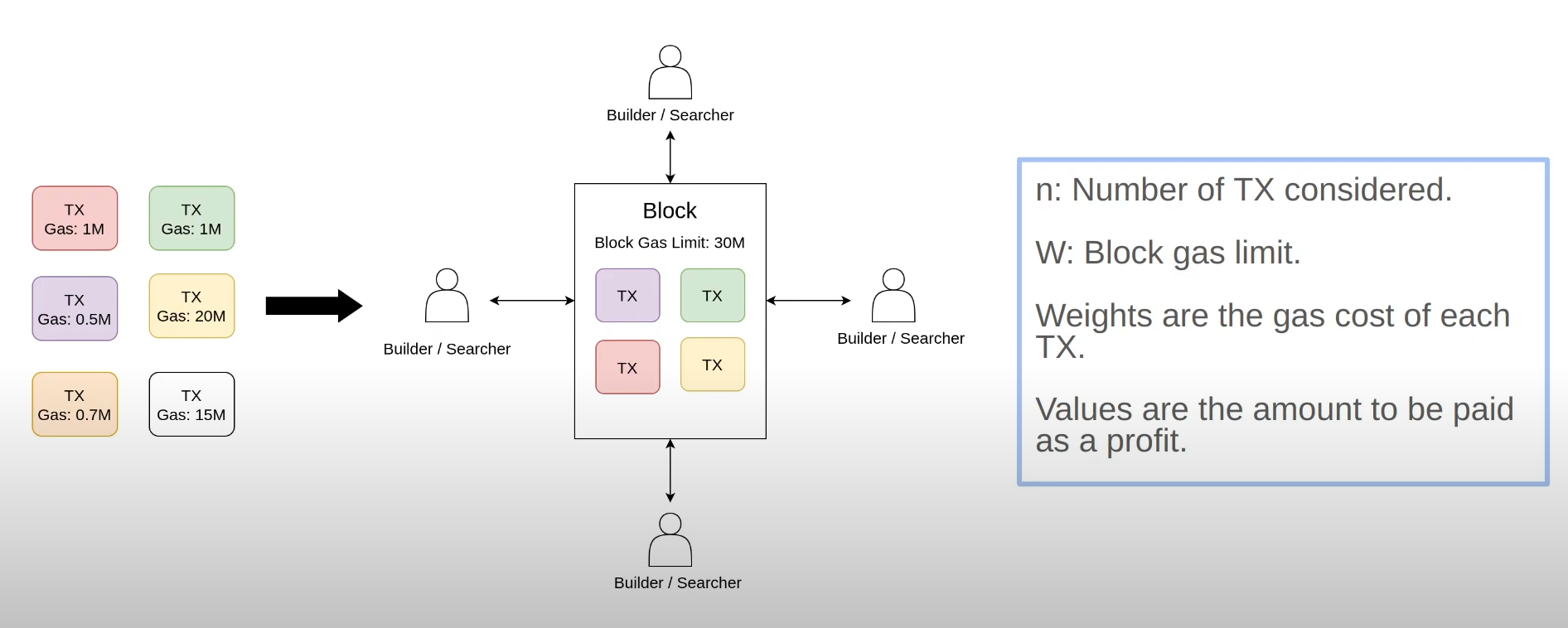
The knapsack problem works like this : you have a knapsack that can carry a certain maximum weight, and you have various items with weights and values.

The goal is to fill your knapsack with the items that have the maximum total value while keeping the total weight under the knapsack's limit.

For blockchain block building, Fernand proposes treating:

• Transactions as "items"
• The gas cost of each transaction as the "weight"
• The transaction fee as the "value"
• The block gas limit as the knapsack's "weight limit"

The goal would be to select the set of transactions with the maximum total fees that fit under the block gas limit. This would allow more computers to participate in selecting transactions for blocks in a decentralized way.

Main ideas (2:45)

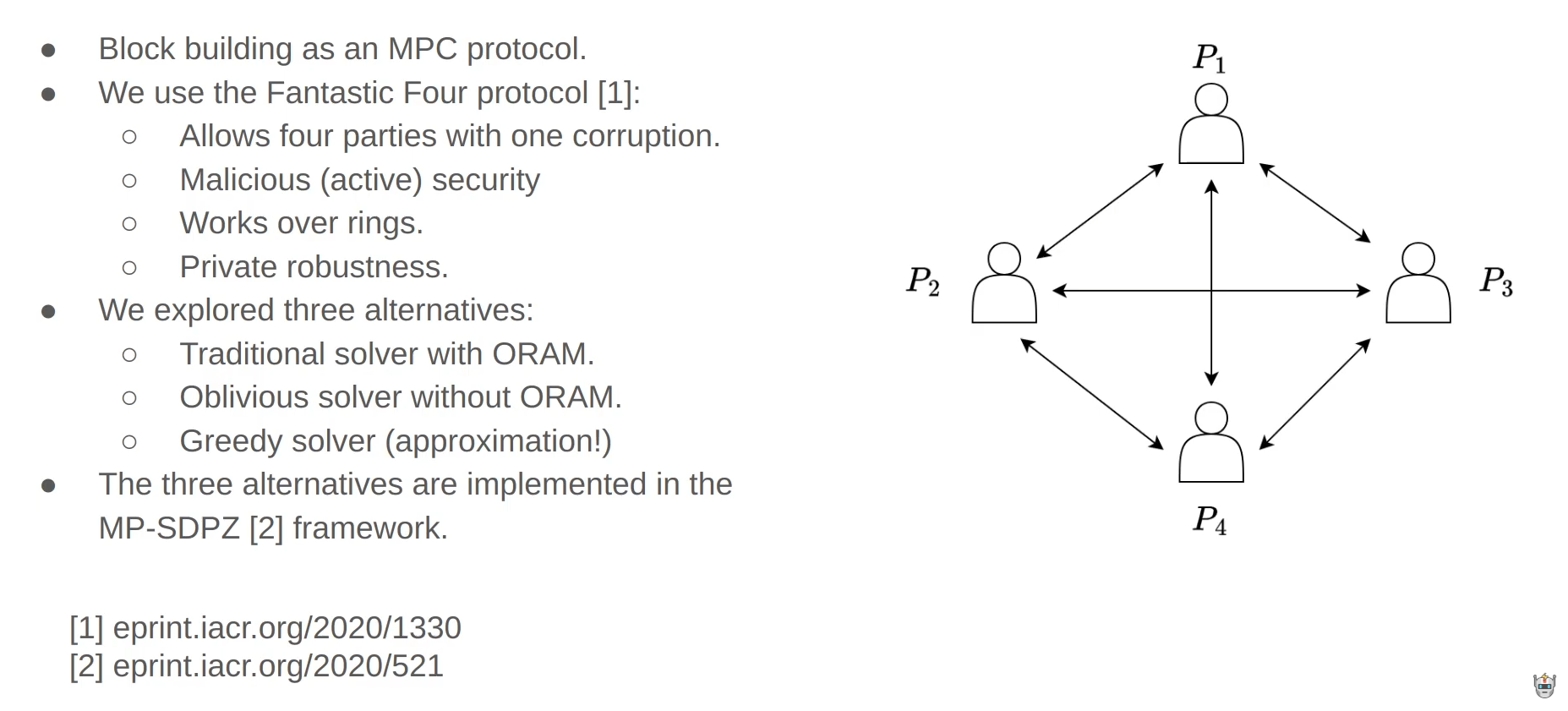
Fernand wants to use a secure multi-party computation (MPC) protocol called "Fantastic Four" to solve the blockchain knapsack problem in a decentralized way.

In this protocol, Several different nodes on the network would participate in building each block. Each node would privately submit to the protocol :

• A set of candidate transactions for the block
• The gas cost and transaction fee of each transaction

The block gas limit is public information.

The Fantastic Four protocol allows 4 nodes to jointly compute functions on private data in a secure way, even if 1 of the nodes is malicious.

Specifically, Hernan plans to represent the knapsack optimization algorithm as an "arithmetic circuit" : The Fantastic Four protocol would evaluate this circuit on the nodes' private inputs in a secure, distributed way. This allows the nodes to jointly solve the knapsack problem without revealing their private transaction sets.

Three alternatives of solving knapsack (5:25)

Hernan explored 3 alternatives to implement the knapsack optimizer in the multi-party computation protocol :

Basic solver :

• Uses the standard dynamic programming algorithm for the knapsack problem
• Stores the intermediate results in an "oblivious RAM" which is a special distributed data structure that keeps data private
• The problem is, with realistic blockchain parameters it would take 2.4 days to build one block, which is very slow.

Shifting solver :

• Improves on the basic solver by getting rid of the oblivious RAM
• It uses a "shifting" method to hide the intermediate data instead of ORAM
• It would take 23 hours for one block. It's faster, but still too slow for practical use

Greedy Approximation Solver :

• It doesn't find the absolute optimal set of transactions, but finds an approximately optimal solution very quickly
• Uses oblivious sorting to hide the transactions
• It takes only 64 seconds for one block which is very fast, and scales well as the number of transactions increases

Conclusions & Observations (7:50)

Overall, the "Greedy Approximation Solver" using the Fantastic Four protocol was the fastest and most practical way to solve the blockchain knapsack problem. Even though it doesn't find the single best set of transactions, it finds a nearly-optimal set very quickly (in 64 seconds).

The main reason it's so much faster is because the Fantastic Four protocol is efficient at doing comparisons between transaction sets, which is the main operation needed for the knapsack problem.

However, finding an exact, optimal solution that is as fast as the approximation algorithm is still an open challenge. And there are other open questions :

• How to model more complex real-world conditions around transaction fees and gas costs into the knapsack algorithm ?
• How to distribute rewards to all the nodes who participate in the multi-party computation, to incentivize a decentralized network ?
• Whether specialized versions of the Fantastic Four protocol could make the solution even faster ?

But overall, this research shows the promise of using multi-party computation to decentralize and optimize blockchain transaction ordering and block creation.

Hernan and his team have continued improving on these results since initially publishing them : https://collective.flashbots.net/t/frp-10-distributed-blockbuilding-networks-via-secure-knapsack-auctions/1955